Python Machine Learning: Linear Regression (I)

Have you ever felt your phone hears your conversation? For example, you and your friend are talking about new shoes, and then when you pick your phone up, you get a bunch of ads about it? Or, when you watch a movie or series on Netflix, the next time you get recommendations of your taste? Well, this all is possible thanks to Machine Learning!

If you have not heard about it, let me explain it to you. Machine Learning is a very popular topic nowadays. It is a method to analyze data in analytical performance. Machine Learning helps humans with very complicated topics, such as forecasting bitcoin price. In machine learning, the AI model learns from data, analyzes it, and, then, establishes patterns to make future decisions.

In this and in the following tutorials, you will learn the basics of Machine Learning using Python. In this tutorial, linear regression will be explained. Before we start coding, what is linear regression? Well, linear regression is an algorithm where the predicted values have a linear slope. In general, regression is mostly used to find the relationship between the variables and forecasting. In the case of linear regression, this relationship will be linear.

In this tutorial, the linear regression will be made using matrix multiplication. If we remember our high school Math lessons, a linear relationship between the dependent and independent variables has the form: y = c₀*x⁰ + c₁*x¹  or y = c₀ + c₁*x, where c₀ will be the intercept with the y-axis, and c₁ - the slope of the line.

This relationship can be expressed in a matrix way. In the system, we will have 3 matrices. The first one will be the values of y, the second one will be a set of x (in this case we will have only x⁰ and x¹) known as Vandermonde matrix, and the third matrix will consist of the coefficients of x (c₀ and c₁). 

Said this, let's start coding! For this tutorial, the y- and x-values are in a text file named 'points.txt' saved in the same directory as your Python file, The first thing we should do is to import the x- and y- values from the text file into Python. As you already learned in the previous tutorial, data can be imported into a DataFrame using the pandas library. However, in this case, we will import the data into an array using the numpy library.

#Importing libraries

import numpy as np

#Importing text file

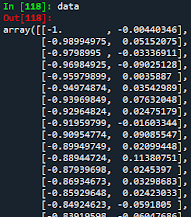
data = np.loadtxt('points.txt', skiprows=(2), dtype=float)

print(data)

The picture above shows a small part of the whole data. As you can notice, it is a 2D-array where the x- and y-values are delimited by the comma (right and left respectively). To have an idea how these data look like, let's first set our x- and y-values and then, plot them. For this, we will use the matplotlib.pyplot library.

#Importing libraries

import matplotlib.pyplot as plt

#Setting x- and y- values

x = data[:,0]

y = data[:,1]

#Plotting data

plt.plot(x,y,'o')

plt.title('Original data')

plt.xlabel('x')

plt.ylabel('y')

plt.show()

Now, let's define our Vandermonde matrix. In linear algebra, a Vandermonde matrix is a matrix with terms of a geometric progression in each row:

x10	x11	x12	x13	...	x1d
x20	x21	x22	x23	...	x2d
x30	x31	x32	x33	...	x3d
...	...	...	...	...	...
xn0	xn1	xn2	xn3	...	xnd

 Notice that d stands for the degree of the polynomial, and n stands for the number of x-values. In this case, since we have a linear relationship, our Vandermonde matrix will be:

1	x1
1	x2
1	x3
...	...
1	xn

Please note that the Vandermonde matrix has dimensions nx2 (n rows and 2 columns). In Python, we will build it in the following way:

#Vandermonde matrixv = np.vstack((np.ones(len(x)),x)).Tprint(v)

How to understand the code above? Well, first we create the column-vector of 1s. Remember that the number of 1s in that column is the same as the x-values. To do so, we use the function np.ones. Then, the second column is exactly as the already defined x-array. Finally, the function np.vstack is used to join these two arrays into one. 
But, be careful! After doing this, we will get a matrix of 2xn (2 rows and n columns). To make this matrix have a dimension nx2, we should transpose it. In Python, this is done using .T function. If we run the code above, we will get the Vandermonde matrix.

To check the dimensions of the array, we use the function shape.

#Checking dimensionsdimensions_v = v.shapeprint(dimensions_v)

Now, it is time to find our coefficients! Like for x, we will express the coefficients as a matrix. To do so, let's remember a bit of linear algebra. Since the goal is to minimize the mean square error of the system, the coefficient matrix will be defined as:

Let's write the above formula in Python.

#Defining the coefficient matrixcoeff = np.linalg.inv(v.T.dot(v)).dot(v.T).dot(y)

In Python, the inverse of a matrix is written using the function np.linalg.inv( ), and in order to multiply matrices, it is necessary to use the function .dot( ), otherwise, if you type the common symbol for multiplication '*', you will get an error. If we print the variable coeff, we will get an array consisting of all the coefficients (in this case only c₀ and c₁)

#Printing the coefficient matrixprint(coeff)

The final step is to build the linear relationship. For this, we will just write the formula which describes this relationship.

#Setting the linear relationshipy_lineal = v.dot(coeff)print(y_lineal)

In order to know how the straight line through all the initially given x- and y- values looks like, let's plot.

#Plotting
#Initially given x- and y-pointsplt.scatter(x,y)
#Linear regression pointsplt.plot(x, y_lineal, color='red')
#Naming the graph, x- and y-axisplt.title('Matrix multiplication')plt.xlabel('x')plt.ylabel('y')
plt.show()

Notice that the blue points are the initially given x- and y-values and the red line is the linear regression we just learned. 
The final Python code will look like this:

Congratulations! You just made the first steps to machine learning! In the next tutorial, you will learn how to make linear regression using a Machine Learning Python library.